Most people expect differentially expressed genes (DEGs) as high at one condition and low at the other, like single factor model below. But it's unrealistic to highly complex biological phenomena. It's worth remembering how genes may behave in the following very simple biological models.
1 Parameter
Model1: Single Factor Model
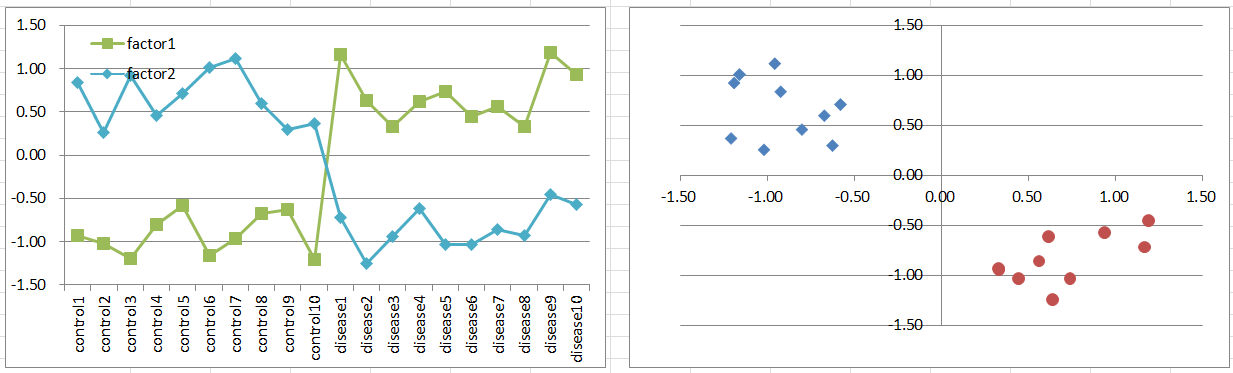
Let's say a disease occurs if the causal gene is highly or lowly expressed. This might be typical you expect, but it's rare in reality.
Control and diseased samples are separated one-dimensionally on expression level of the gene.
2 Parameters
Model2: Two Factors Model
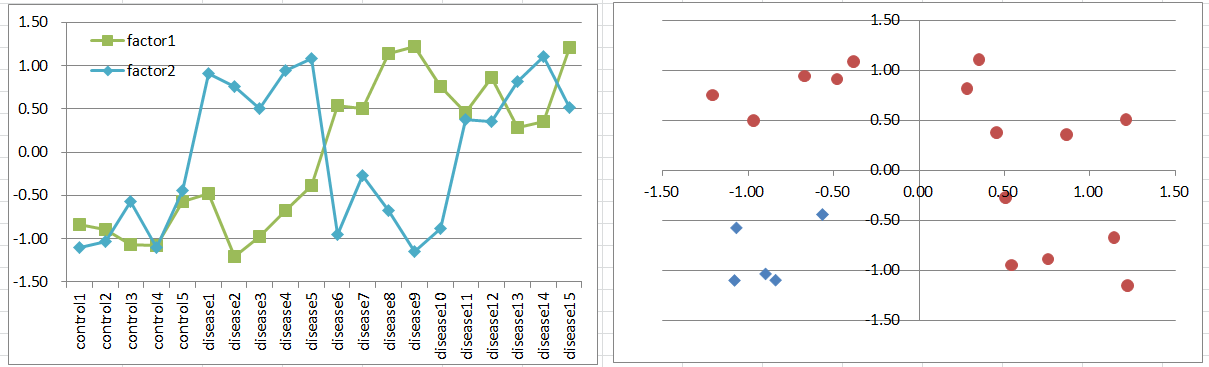
Let's say a disease occurs when either one of factors is highly expressing. They can be homologues or different input paths of a pathway. Notice that control samples are less than disease, if you had samples balanced; of course it's not likely to happen.
Expression levels can be bimodal in disease samples, and you can't expect normal distribution which is a basic assumption of t-test. But still, it's likely you can extract such genes with small p-values.
Diseased samples are in 3 quadrants of the 2D coordinate plane, and controls are in 1/4.
Model3: Co-factors Model
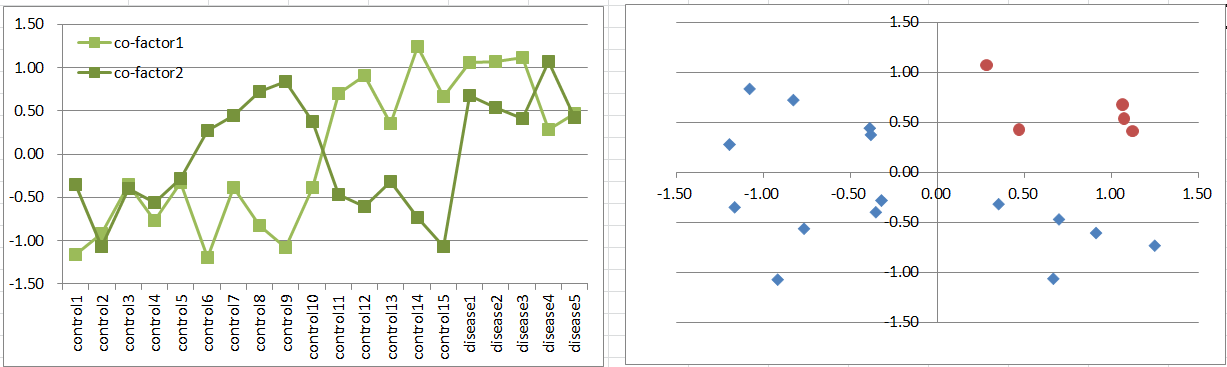
Let's say a disease occurs when both of co-factors are highly expressing. It's a simple and general model in biology.
This is similar to model2, but disease samples are far less. It also violates t-test assumption, but still it's likely to work to extract co-factors as DEGs.
Diseased samples are in one quadrants of the 2D coordinate plane.
Model4: Factor + Inhibitor Model
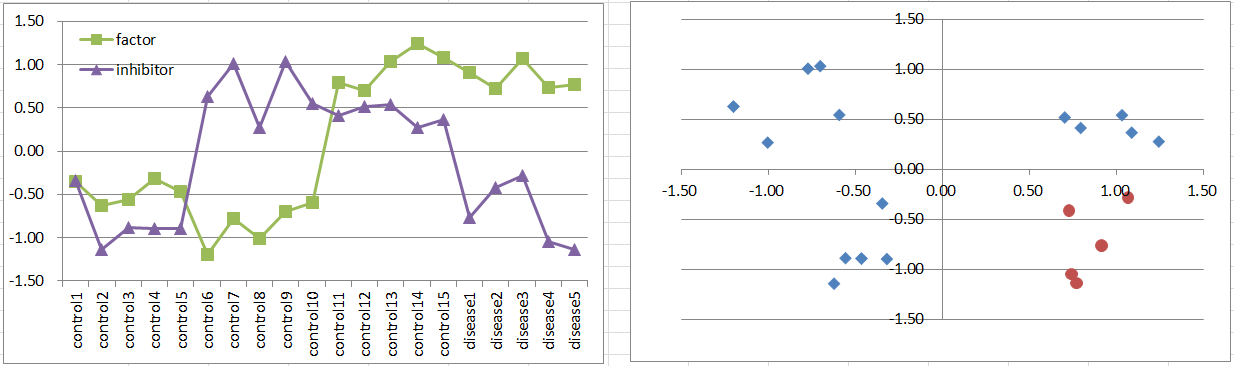
Let's say a disease occurs when the factor is highly expressing, but it's suppressed if the inhibitor is also expressing. It's also a simple and general model in biology.
This is similar to model3 in frequency and the pattern on the 2D coordinate plane.
Model5: 2 Balancers Model
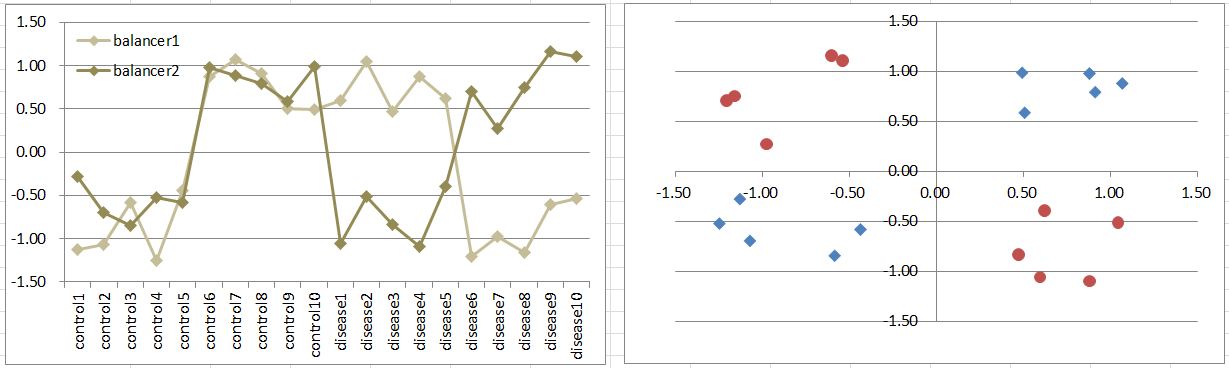
Let's say a disease occurs if the expression levels of the 2 genes are different, regardless of expression levels. Imagine that there are incoming signals continuously to a pathway. And they're usually balanced. A break of the balance takes the condition away from the normal. It's also a simple model of dynamics.
Diseased samples are in 2 quadrants diagonally. It's difficult to extract such gens by t-test because they're not differently expressing between the conditions. But still simulation of p-values are often less than 0.05! Download to see t-test p-values.
Model2-5 are similar. Differences are in frequency and locations in the 2D coordinate plane of disease samples. The following models are expansion of them to 3 parameters.
3 Parameters
Model6: 2 Factors + Inhibitor Model
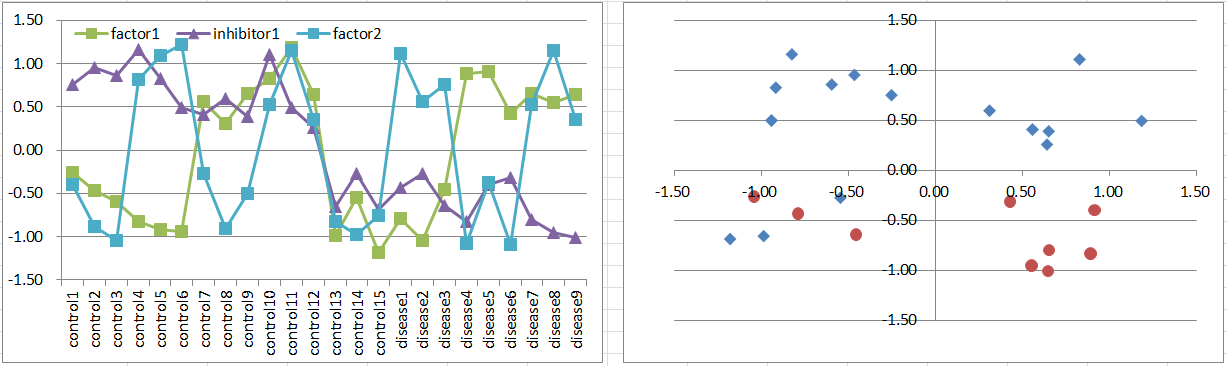
Let's say a disease occurs if either one of factors is highly expressing. But it's suppressed if the inhibitor is also expressing.
It's more difficult to extract factor genes by statistical test, while you can extract inhibitors.
Diseased samples are in 3 octants of the 3D coordinate space.
Model7: Factor + Co-inhibitors Model
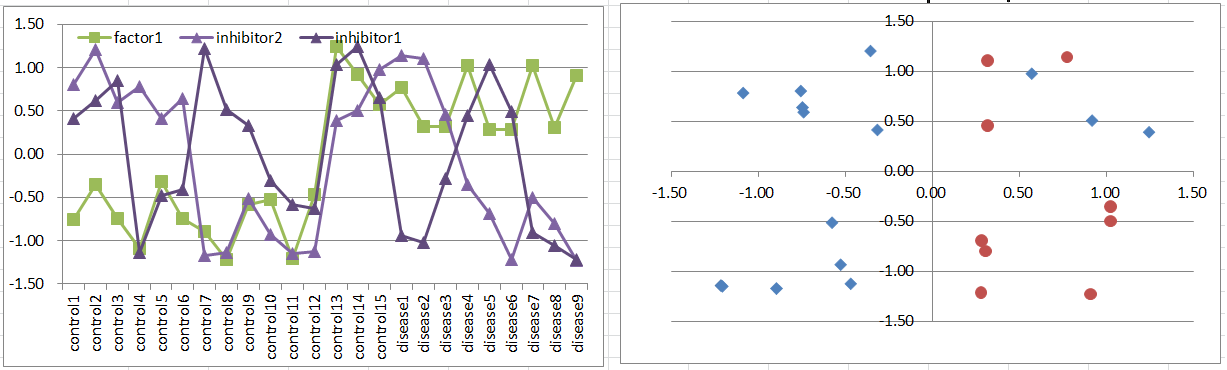
Let's say a disease occurs when the factor is highly expressing. But it's suppressed if both of co-inhibitors are expressing.
Notice that this pattern is quite similar to model6.
Model8: Co-factors + Inhibitor Model
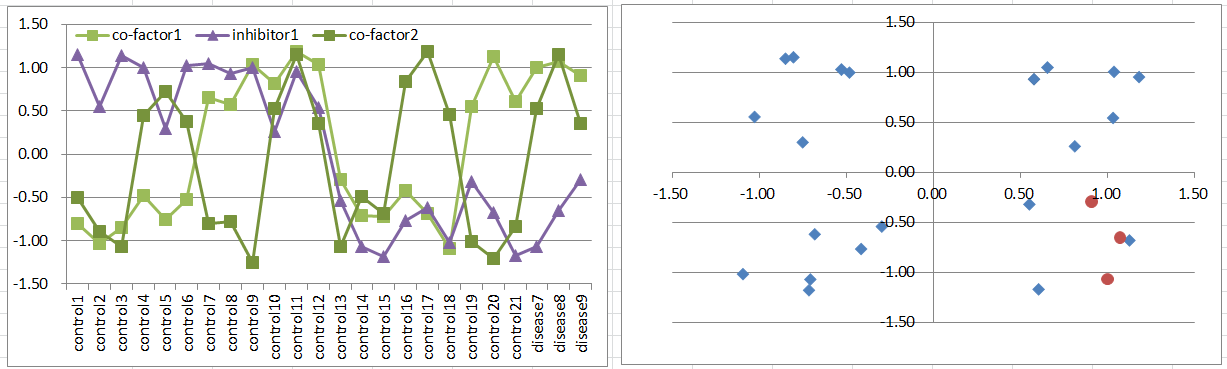
Let's say a disease occurs when both of co-factors are highly expressing. But it's suppressed if the inhibitor is expressing.
This disease type must be much rare than model6 or 7. Disease samples are only in one of octants of the 3D coordinate space.
Model9: Factor + 2 Inhibitor Model
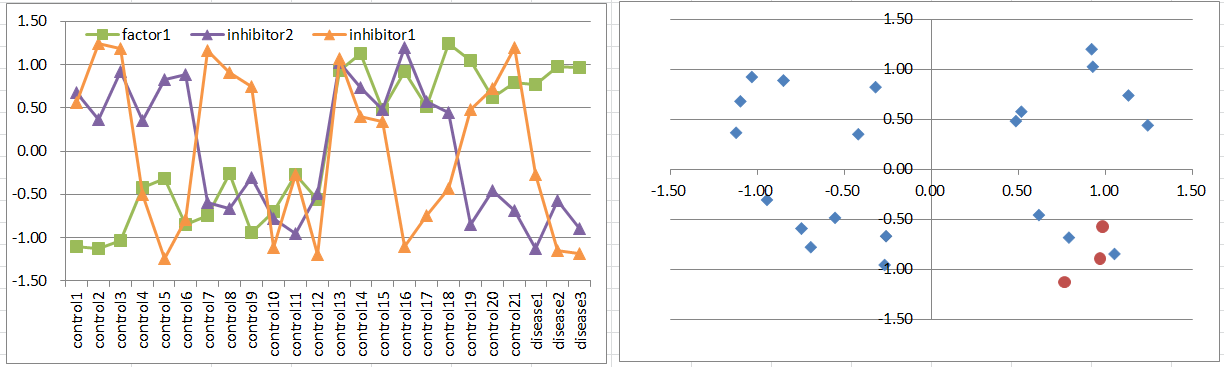
Let's say a disease occurs when the factor is highly expressing. But it's suppressed if one of inhibitors is expressing.
This pattern is quite similar to model8.
Model10: 3 Balancers Model
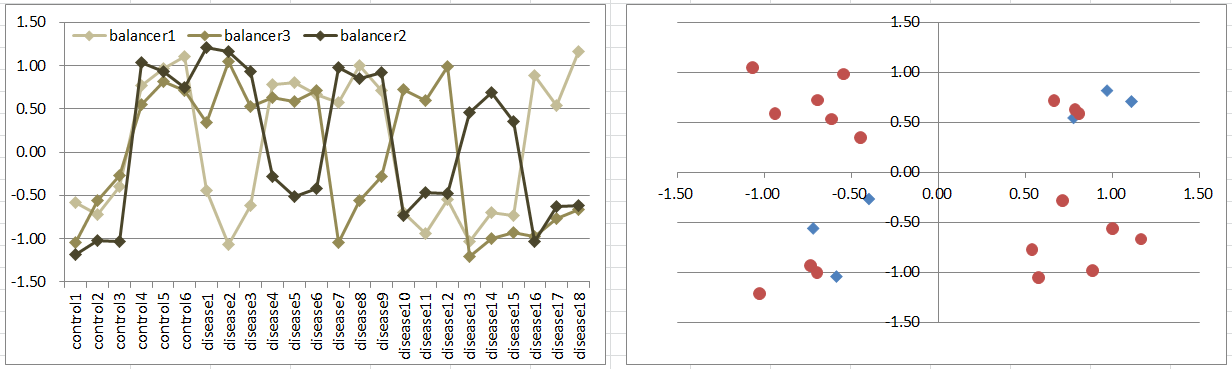
Let's say a disease occurs if one of 3 balancing genes is differentially expressing to other two regardless of their expression levels.
This is similar to model5, while controls are in 2 diagonal octants of the 3D coordinate space.
Download the Excel file of this simulation from DropBox.
Conclusion
Notice that Model 3&4, 6&7, 8&9 and 5&10 have same patterns. It indicates apparent patterns of gene expression profiles are less than possible mechanisms. It's a good news, isn't it? You don't need to refer all different models. If you see the scatter plots of models, which has less variations. It's not realistic to get balanced samples like models. Usually you'll have more disease samples. Computer can generate enormous possible models, but it can't figure out which is likely to be true. Only researchers who know even subtle parameters which couldn't be data can do it.
Now you know that searching DEGs will give you a list of genes downstream, but it won't give you causal genes. But still, the simple t-test is useful because you can collect candidates by filtering p-values at non-stringent cutoff between 0.05 and 0.1. Don't stick to genes at very small (significant) p-values.